在這項工作中,對具有高能量和動量分辨率的獨立石墨烯進行了電子能量損失譜(EELS),以解開接近光學極限的狄拉克電子激發間隙的準彈性散射。通過將測量的EELS與理論水平不斷提高的從頭計算進行比較,本研究展示了有限傳遞動量下多體效應對電子激發的重要性。在GW近似和Bethe–Salpeter方程中分別討論了準粒子校正和激子效應。這兩種效應在EEL光譜的描述中都是至關重要的,以獲得與實驗的定量一致性,激發間隙和π等離子體激元的位置、色散和形狀都受到激子效應的顯著影響。

圖1. 30keV下獨立石墨烯的TEM圖像和衍射圖案:(a)低放大率TEM圖像;(b) 高分辨率TEM圖像;(c) (b)中的高分辨率圖像的FFT;(d) 在40cm的相機長度處獲得的500nm寬光束的衍射圖案。
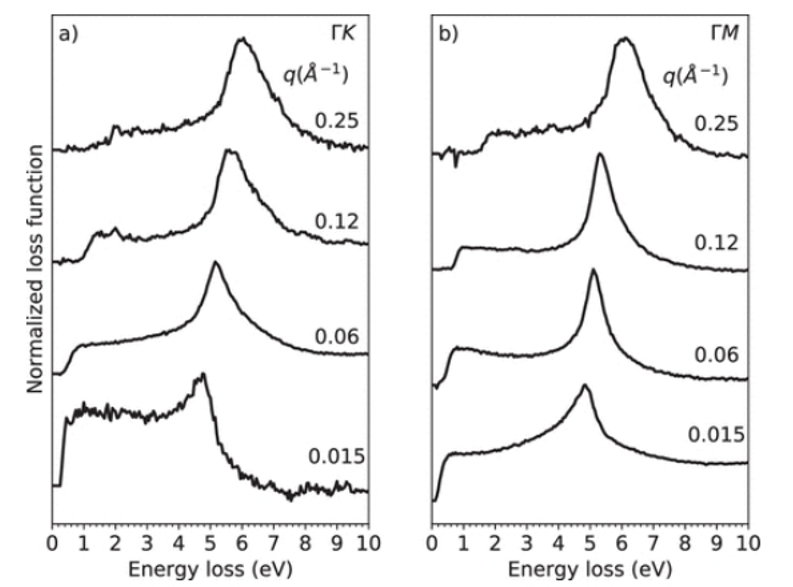
圖2. 測量了沿ΓK(a)和ΓM(b)方向取向的不同動量轉移q的獨立石墨烯的低能量損失譜。零損耗峰值已被刪除。
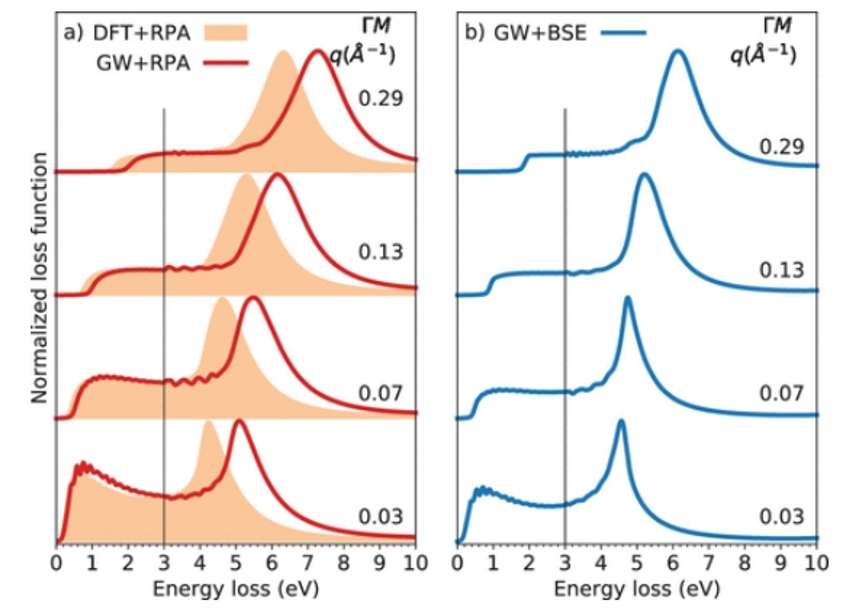
圖3. 在不同理論水平上計算的沿ΓM增加動量傳遞時獨立石墨烯的能量損失譜:DFT+RPA和GW+RPA(a);GW+BSE(b)。
.png)
圖4. (a) 通過支持信息中描述的程序獲得的π-等離子體色散。黑色(藍色)的直線是測量(計算)的等離子體色散的線性回歸。虛線是眼睛的向導。(b,c)在沿ΓM方向的不同動量轉移下,測量和計算的獨立石墨烯的π-等離子體激元峰:(b)q=0.06Å-1;(c) q=0.13Å–1。不同的顏色指的是計算中不同的理論水平:DFT+RPA(橙色線)、GW+RPA(紅色線)和GW+BSE(藍色線)。實驗數據顯示為黑色恒星。
.png)
圖5. (a) 在不同理論水平上計算的獨立石墨烯沿ΓM方向的起始色散。(b) 實驗和計算的起始形狀為q≈0.2Å-1。灰線表示用于確定起點的半高切線。實心圓表示起始位置。(c) ΓK和ΓM方向上的q的測量原點。由于經驗的不確定性,尚未在ΓK方向上進行提取。ref(10)(q≤0.4)Å–1的起始不可及區域被染成紅色。它也顯示在石墨烯的第一個BZ內部。(d) 放大測量的起始分散度(黑色),并與計算的起始分散比較(藍色)。不可訪問范圍q≤0.05)Å–1被染成灰色,也顯示在第一個BZ中。石墨烯的第一個PZ上也繪制了相同的區域。q≤0.05Å-1范圍內的灰色數據點有很大的誤差,因為它們取決于ZLP的去除。
相關研究成果由羅馬第一大學Alberto Guandalini等人2023年發表在Nano Letters (鏈接:https://doi.org/10.1021/acs.nanolett.3c03863)上。原文:Excitonic Effects in Energy-Loss Spectra of Freestanding Graphene
轉自《石墨烯研究》公眾號




.png)
.png)


