研究了石墨烯板增強(qiáng)泡沫金屬(GPLRMF)矩形板的非線性強(qiáng)迫振動(dòng)。人們對(duì)這種新型納米復(fù)合材料結(jié)構(gòu)的主、超諧波和次諧波共振進(jìn)行了研究。考慮了三種石墨烯片(GPL)模式和三種孔隙度分布。基于von Kármán非線性板理論，通過(guò)Hamilton原理得到了GPLRMF板的控制方程和一般邊界條件。通過(guò)引入應(yīng)力函數(shù)，用伽遼金法得到了板的非線性常微分方程。然后，采用多尺度法求解了GPLRMF板的頻率響應(yīng)和力響應(yīng)關(guān)系;并進(jìn)行效度研究以驗(yàn)證本方法的有效性。結(jié)果表明，GPLRMF板在主共振和超諧共振中表現(xiàn)出硬化非線性。在主共振和超諧共振中，在中間表面分散更多的小孔隙或更多的GPLs將導(dǎo)致板的振幅和共振域更大。而均勻分布的孔隙或均勻分布的GPLs在次諧波的情況下會(huì)導(dǎo)致較大的振幅。此外，孔隙率系數(shù)或GPL質(zhì)量分?jǐn)?shù)的變化可以顯著改變GPLRMF板的非線性動(dòng)力學(xué)行為。
.png)
圖1. GPLRMF矩形板和不同的孔隙率分布。
.png)
圖2. GPL不同分布模式。
.png)
圖3. 簡(jiǎn)支各向同性方板主共振頻響曲線比較。
.png)
圖4. 不同孔隙度分布時(shí)的主共振頻響曲線。
.png)
圖5. 不同GPL時(shí)的主共振頻響曲線。
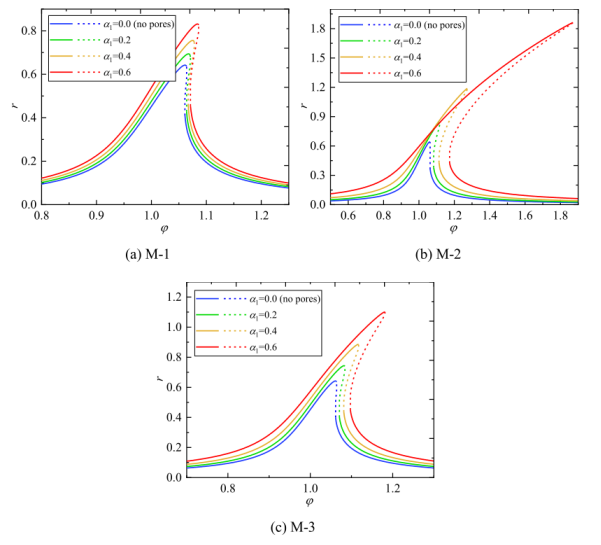
圖6. 不同孔隙率系數(shù)時(shí)主共振頻響曲線。
.png)
圖7. 不同GPL重量分?jǐn)?shù)W
G時(shí)主共振的頻響曲線。
.png)
圖8. 不同GPL時(shí)主共振力響應(yīng)曲線。
.png)
圖9. 不同孔隙度分布下超諧波共振的頻響曲線。
.png)
圖10. 不同GPL時(shí)超諧波共振的頻響曲線。
.png)
圖11. 不同孔隙率系數(shù)時(shí)超諧波共振的頻響曲線。
.png)
圖12. 不同GPL重量分?jǐn)?shù)W
G時(shí)超諧波共振頻響曲線。
.png)
圖13. 不同GPL時(shí)超諧共振力響應(yīng)曲線。
.png)
圖14. 不同孔隙度分布下的次諧波共振頻響曲線。
.png)
圖15. 不同GPL時(shí)次諧波共振頻響曲線。
.png)
圖16. 不同孔隙率系數(shù)時(shí)次諧波共振頻響曲線。
.png)
圖17. 不同GPL重量分?jǐn)?shù)W
G時(shí)次諧波共振頻率響應(yīng)曲線。
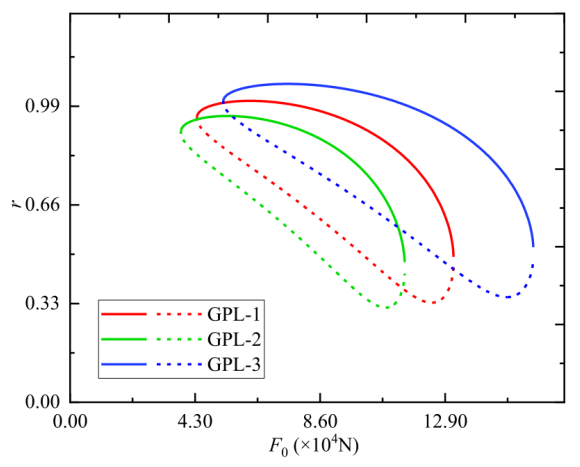
圖18. 不同GPL時(shí)次諧波共振力響應(yīng)曲線。
相關(guān)研究成果由東北大學(xué)力學(xué)學(xué)系、東北大學(xué)深部金屬礦山安全開采教育部重點(diǎn)實(shí)驗(yàn)室Mei Wen Teng和Yan Qing Wang等人于2021年發(fā)表在Thin-Walled Structures (https://doi.org/10.1016/j.tws.2021.107799)上。原文：Nonlinear forced vibration of simply supported functionally graded porous nanocomposite thin plates reinforced with graphene platelets。
轉(zhuǎn)自《石墨烯研究》公眾號(hào)
.jpg)
